Some notes on Chapter 6: How the Quantum Was Forced on Physics Thermal radiation
(Planck): To see why we don’t see quantum effects in everyday stuff, we calculate and contrast the energy steps relative to the total energy for a vibrating electron and for a child on a swing. (We use E = kT, with a bit of hand waving, for the electron’s total energy.)
Photoelectric effect (Einstein): We emphasize (with evidence) how unlikely it would be for the spread out energy of a light wave to kick an electron out of a metal. We use the analogy of knocking cans off a fence with a tossed stone and failing to do so with an extended blast of air with the same energy. Explicitly using Einstein’s postulates for photons (i.e., one photon, E = hf, totally absorbed by a single electron) we derive the photoelectric equation by analogy to the superman and car-in-a-dip story in the conservation of energy example in our Chapter 5 comments.
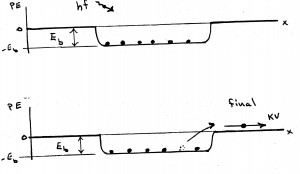
mv^2/2 = hf – Ebinding We note that the slope is h, which appears here for the first time beyond thermal radiation. We present the strong arguments for and against (i.e., interference) the photon hypothesis to establish that there is a mystery here.
Stable atom (Bohr): After discussing the Brownian motion argument for the existence of atoms, we note the problem of the instability of the planetary atom. We go through the mathematics of orbital motion, Bohr’s postulate of quantized angular momentum, and derive the energy spectrum of hydrogen. (We skipped discussing the 1/r potential in Chapter 4 to treat it here along with Bohr’s atom, where there is more motivation. We include more math in this chapter than in any previous or later one.)
Matter waves (de Broglie): We do the bit of algebra showing how de Broglie’s wave postulate leads to Bohr’s quantization formula. To emphasize that the wave whose wavelengths fit around a Bohr orbit are not wiggles of an electron in space, we draw the perspective sketch where we emphasize that the “vertical” axis is the amplitude of the de Broglie wave. (Exactly what is the de Broglie wave? He didn’t know. It’s now essentially almost the wavefunction, but what exactly that is we still don’t really know.) (The de Broglie-Bohm “pilot wave” is something later and different, an interpretation of quantum mechanics we discuss in Chapter 10.)