Some notes on Chapter 4: All the Rest of Classical Physics
Chapter 4 covers interference, electromagnetic fields, energy, and relativity. We’ll here also add a comment on momentum.
Interference: The geometric treatment of interference is tricky, and few conceptual physics will remember it. That’s OK; it’s the wave concept, not the geometric argument, that is critical to understanding the quantum enigma.
While interference is the demonstration that an entity is a spread out wave (coming from more than one source), the evidence is indirect; it’s circumstantial. We never actually see the crests and troughs of a light wave. We infer the wavy “spreadoutness” from the pattern on the screen.
That inference can be made explicit. That the light came from both slits can be convincingly argued by noting that the pattern spacing, d, depends on the spacing, s, of the slits. I.e., d = f(s). That dependence is something students can remember, even if they can’t reproduce the geometry of interference.
Incidentally, we always assume the slits are small enough that we can ignore single-slit diffraction.
The disappearance of the interference pattern when only a single slit is open is analogous to the opening of a single box of a pair discussed in Chapters 7 and 9.
Electromagnetic force: In addition to the usual aspects, such as Coulomb’s law, we emphasize the physical reality of the electric and magnetic fields–even though we can’t see them. Electromagnetic waves even exert force, radiation pressure, which could, for example, propel space vehicles. In a later chapter we make the point that the wavefunction is not a physically real field in this classical sense.
Momentum: We say nothing about momentum conservation in this chapter. But we do treat its conservation in one-dimensional collisions in our conceptual physics course. We use the example of colliding railroad cars. A special simple case (total momentum = 0) arises in the introduction to EPR (page 128). We also treat conservation of angular momentum, which later comes up in the Bell’s theorem experiments.
Energy: In lectures we deal with the conservation of energy using an analogy to the piggy bank. (The final money in the bank equals the original money plus the money added.) We formulate energy conservation with the “piggy bank equation”: Efinal = Einitial + Eadded, emphasizing that any of these energies can be positive or negative. We use an example of energy conservation that is analogous to the way we later treat the photoelectric effect. Superman gives the car a push. If his push adds more energy, Eadded, than the (negative) energy with which the dip holds the car (- mgh), the car rolls out of the dip, and has kinetic energy mv^2/2. (We used negative potential energy earlier in treating planetary motion.)
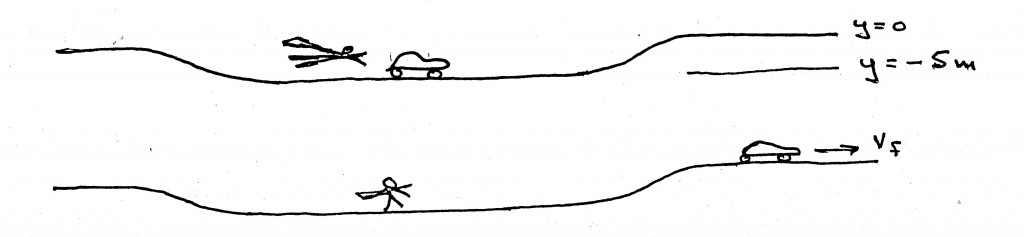
mv^2/2 = Eadded – mgh
(Analogous to mv^2/2 = hf – Ebinding, the photoelectric equation.)
Relativity: All we would really need to say about relativity (in our later presentation of Bell’s theorem) is that it has been established that no physical interaction, no information, can travel faster than the speed of light. Nevertheless, we devote two full lectures to special relativity at this point.
One reason for this is that it’s very interesting to students. Another reason is that special relativity beautifully displays the power of a logical argument: From only the very-reasonable assumption that the laws of physics are the same in all inertial frames, and the not-so-reasonable assumption, but an assumption accounting for the Michelson-Morely result, that the speed of light is the same in all inertial frames, we very simply derive the fantastic properties of time and space.
However, our most important reason for presenting relativity in our conceptual physics course is that it is practice in believing “impossible” things. It is very effective psychological preparation for the quantum enigma.
In the draft text for our course, “The Quantum Enigma,” we have two chapters on Special Relativity. You may download them and use them in any way you wish.